目录

第七章

反引力场实验(续)

（ More about antigravitational experiments）

　

7.1 多狗雪橇式的飞碟

一个人造飞碟可以由多个反引力场发动机来拖曳,这些发动机可以分摊 |Σa'| (见第一章或第二章中的反引力场发动机方程组),也就是分摊飞碟的阻力,就像很多狗拉一个雪橇那样.

但是每个反引力场发动机的运动具有不确定性,就像未经过良好训练的雪橇狗那样.

　

7.2 反引力场发动机的加速度和速度

7.2.1 反引力场加速度是德布罗意波的加速度

反引力场发动机方程组中的a是反引力场发动机的德布罗意波的加速度^[1].

[1] Peter R. Holland. 运动的量子理论.世界图书出版公司北京公司,2001年4月.第262页.

7.2.2 速度

根据量子力学,在第四章的最后一幅图中,如果波长λ → 0,那么在一个给定的区域,飞碟的速率(不是速度)与这个区域的波函数绝对值的平方的平均值成反比例(这个波函数不是以这个区域的数值,而是以初始点的数值作为其边界条件的一部分的);而且当λ → 0时,粒子在这个区域的平均速率| v |与经典力学中的速率是一致的;因此根据7.2.1节可以得到

|v_t| ≈ |v₀| + |a t| ,     (λ → 0) ,

式中的量都取这个区域的数值.

　

7.3  在势垒附近

7.3.1 人造飞碟

产生 | Σa' | 的物体可以成为势垒.地面、海面、云、山和气流等障碍物都有可能成为势垒,并且使得飞碟的引物(引力场物质)团大粒子的德布罗意波成为势垒区域中的波函数.根据量子力学,势垒区域中的波函数具有节点,除非这个波函数处于基态.

7.3.2 类似的事实

当UFO位于势垒附近时,UFO常被看到一蹿一蹿地运动、停滞或往返运动.

7.3.3 自转体转速慢的飞碟反而有可能飞得较快

根据第四章所描述的实验可以知道,当自转体转速较小时,它的引物团大粒子的质量较小,根据量子力学,"小船"具有势垒穿透效应的相对概率较大.

因此在实验中,有时虽然自转体的转速较小,但由于"小船"具有势垒穿透效应,船速有可能大于自转体转速较快时的船速,并且小船的运动轻快均匀,与时快时慢、一蹿一蹿的运动形成了鲜明的对照.

7.3.4 量子尺寸效应与飞碟的运动

在实验中,水的阻力对"小船"形成势垒.由第四章可以知道,自转体转速慢的小船的运动的波长较长,因而运动的量子尺寸效应较强,小船动量的不确定程度较大,运动的量子化现象较明显.相反,自转体转速快的小船的运动的量子化现象较不明显.

势垒附近的飞碟的运动也是这样.

7.3.5 对于势阱壁的作用力

根据量子力学,粒子作用在势阱壁上的平均力是

< F > = 2 En / L ,

式中< F >是平均力, En是粒子的能量, L是势阱的宽度.势阱壁越高,公式就越准确^[1].

第四章的最后一幅图显示出,引物团大粒子的最后一个波长大约是1.2*10^-3m,这时量子现象明显.因此,根据第7.3.4节,水阻力形成的势阱的宽度L大约是1.2*10^-3m.从第四章可以知道En 是 1.77*10^-34 J .

因此

<F> = 2 * 1.77*10^-34 / (1.2 * 10^-3 ) = 2.95 * 10^-31 (N),

即

< F > = 2.95 * 10^-31 N . (1)

现在根据理论力学中的质点运动的微分方程的解来检验这个结论.水的阻力是

F_r = - m (1/ limit v)² a (limit v)² = - m a ,

式中F_r是水阻力, m是引物团大粒子的质量, limit v是它的极限速度,a是它的加速度.

从第4章可以知道, mn = 1.236 * 10^-26 kg, a = 2.192 * 10^-5 ms^-2.因此

当m = mn时有

- m * a = - mn * a = - 2.71 * 10^-31 N ,

即

F_r = - 2.71 * 10^-31 N .

根据牛顿第三定律,作用力是

F = 2.71 * 10^-31 N . (2)

[1] 钱伯初,曾谨言.量子力学习题精选与剖析.第2版.科学出版社,1999年1月.上册,第6页至第7页.

　

7.4  当反引力场工作时飞碟外缘的转速变慢

在实验中,当反引力场工作时,引物团大粒子已经形成,自转体的旋转就与引物团大粒子的旋转联合起来,它们的自转角动量就主要由引物团大粒子之外的引力场物质的角动量来抵消,而不是主要由电动机底座的角动量来抵消,因此第一章和第三章里所描述的实验中的脸盆的自转就变得不那么明显了.

因此当反引力场工作时人造飞碟外缘的转速变慢.

7.5 转速越大,侧向运动的概率就越大

引物团大粒子有沿着它的德布罗意波的波阵面侧向运动的可能性.

因此在第一章描述的实验中"小船"有侧向运动的可能性.

因此人造飞碟有侧向运动的可能性.

当德布罗意波在水阻力形成的势垒之间运动时,就形成了干涉条纹.

如果波长较短,亮条纹就较密,也就是说,概率波的波峰较密,邻近的波峰的高度相似,于是粒子被发现侧向运动的概率就较大.

因此在第一章描述的实验中,自转体转速快的小船比自转体转速慢的小船被发现侧向运动的概率大.

7.6 轨道角动量与自旋角动量

在量子力学中,粒子是作为点粒子来处理的,因此,像电子云那样,引物团大粒子应作为一个点粒子的粒子云来处理,引物团大粒子可以称作引物团子.引物团子的自转是引物团子云的根据波函数的转动,不遵从相对论的质速关系式;因此当计算引物团子的角动量时,引物团子的速度和质量是它平动时的速度和质量.

因此引物团子的总角动量是由反引力场发动机导致的;引物团子的轨道角动量是它的云的轨道角动量;引物团子的自旋角动量是引物团子使它周围的"台阶"产生的自旋角动量(参看第6章第6.8节);这使人想起了李·斯莫林描述的自旋网络^[1].

命J为总角动量,L为轨道角动量,S为自旋角动量.于是有如下关系:

J = L + S . (1)

在第四章所记述的实验中, r = 0.0046m , m0 = 4.62·10^-28 kg , v0 = 6.44·10^-5 ms^-1 . 由于

J = r × m v ,

因此J₀ ,即引物团子的总角动量的初始值,是

J₀ = r × m0 · v0 .

由此

J₀ = 1.3 ħ ;

精确到半个单位,

J₀ = 1.5 ħ . (2)

由轨道角动量的量子化条件和方程(2)可以知道, L₀ ,即引物团子的轨道角动量的初始值,应该是

L₀ = 1 ħ ,

于是S₀,即引物团子使周围的"台阶"(见第6.8节)产生的自旋角动量的初始值,是

S₀ = J₀ – L₀ = (1.5 - 1) ħ ,

即

S₀ = (1/2) ħ .

更一般地,存在着如下关系式:

s = (1/2) ħ' , (2)

其中s是某个引物团子的自旋,即这个引物团子使它周围的"台阶"产生的自旋角动量. ħ'是某个尺度的"台阶"的作用量子. ħ'的数值是通过观测来测量的.

根据不确定关系(见6.8节), ħ'较大的物体的现在时范围较大.这是宇宙中存在着暗物质和暗能量(参看6.4和6.13节)的原因之一.

[1] 李·斯莫林.通向量子引力的三条途径.李新洲,翟向华,刘道军译.上海科学技术出版社,2003年3月第1版.第103页.

7.7 大为增加了的反引力场加速度

反引力场发动机自转体的引物团子的质量很小,因此它的粒子云的概率波的波长很长;由于这个长程的概率波的影响,经过一段时间后,众多电子会作为一个单个的单位像单个粒子那样在波峰附近作整体运动;于是在计算反引力场加速度的时候就要在反引力场发动机方程组(见第一章或第二章)中代入下列方程

m = m_unit ，

式中m_unit 是上述单位的质量.

因为

m_unit > m_e ,

所以反引力场发动机的加速度大为增加.

有时在实验中可以观察到经过一段时间后"小船"突然加速.

有时UFO在空中悬停一段时间后会突然加速.

7.8 反引力场理论的多粒子性和非定域性

张永德指出,量子理论具有多粒子性和非定域性.当一个粒子位于势垒附近时,它的动量变化所对应的能量有可能足以产生新的全同粒子^[1].

因此引物团子和时空的"自旋台阶"具有粒子数不守恒和非定域的性质,服从全同粒子的不可区分原理,这些全同粒子可以位于定域的、非定域的、现在的和非现在的时空之中.

所以实验室内外的某些物体,例如管道,有可能变成反引力场发动机的扰动装置.

[1] 张永德.量子"天龙八部".见朝花夕拾－教与学篇.王文正,柯善哲,刘全慧主

编.科学出版社,2004年10月第一版.

7.9 反引力场中时间有不止一维

在实验中,有时小船在某一个位置的停滞时间过长,其停滞概率远大于第4章依据量子力学所预期的概率,而与实验初始时的停滞概率相似;有时在停滞后小船倒退,就象有时UFO被看到沿原路退回那样;小船的时间似乎又处于初始时刻,甚至似乎倒退了.

这说明在反引力场中,

(1) 时空的"自旋台阶"是自旋的莫比乌斯圈(圆的莫比乌斯带);

(2) 根据第6.8节,这莫比乌斯圈的半径随着时空曲率的增加而增加,因而随着圈的能量的增加而增加;

(3) 时间有不止一维,其中一个时间维的基础由时空台阶的量子化自旋构成,通常的时间是又一个时间维;

(4) 局部的时空可以是曹盛林提出的芬斯勒时空^[1],其中ds⁴是不变量:

ds⁴ = ( c² - v² ) dt⁴ + ( dx² + dy² + dz² )² .

[1] 曹盛林.芬斯勒时空中的相对论及宇宙论.北京:北京师范大学出版

社,2001年8月.

7.10 反引力场作用量子方程

7.10.1 实验

在本次实验中(请参看第四章),自转体的转速是每秒13转,小船前进的最大距离是0.01米,最后一级平均速度是0.00025米/秒,实验时间是67秒,自转体金属部分的回转半径是0.0046米,质量是0.01千克.

以下是用数学软件Mathematica写出的部分程序.

rot=13;xx=0.01;limitv=0.00025;tt=67;r=0.0046;

data=Table[{{0,0},{0.001,17},{0.002,34},{0.003,41},{0.004,45},{0.005,47},{0.006,53},

{0.007,55},{0.008,60},{0.009,63},{0.01,67}}];

使用与第四章相似的程序可以作出如下图形:

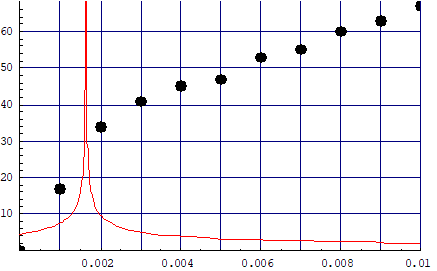
数据看上去是量子化的,但是根据量子力学作出的图形在点0.002以后却是平滑的.这意味着反引力场除了遵循量子力学之外,反引力场还有自己的反引力场作用量子.当具有普朗克作用量子的波峰过稀或过密时,具有反引力场作用量子的波峰就显现了出来.

根据第6.8节和第7.9节,时空台阶的自旋角动量应该与物体的质量、它的引物团粒子的质量和牛顿引力常数G成正比;并且应该与在某处发现物体的概率成正比,因而应该与物体的速率成反比.

根据观测,物质宇宙的73%由暗能量构成.因此时空的自旋台阶的自旋角动量中有73%是以反引力场能量的形式存在的, 27%是通常意义上的角动量.

于是可以建立起下面的方程

h' = 0.27 G M m_gfm / v , ( 1 )

式中h'是反引力场作用量子, M是被反引力场拖曳的物体的质量, m_gfm是这个物体的引物团粒子的质量, v是这个物体的速率.根据胡宁的理论(见第四章注解[1]),

m_gfm ≈ M v² / c² . (2)

由( 1 )和( 2 )式可以得到如下方程:

h' = 0.27 G M (M v² / c² ) / v ,

h' = 0.27 G M² v / c² . ( 3 )

方程( 3 )可以叫做反引力场作用量子方程.

根据1998年国际推荐值,G = 6.673 × 10^-11 m³kg^-1s^-2 , c = 299792458 ms^-1.

在第四章第一幅图下面的程序中,将普朗克常数替换为h',将h1替换为h'/(2*Pi),将5.521替换为9.023, 将nt = 10 替换为nt = 17,然后进行计算,得到

h' = 5.01168 × 10^-36 m² kg s^-1 ,

作出的下面的图形与数据符合得较好.

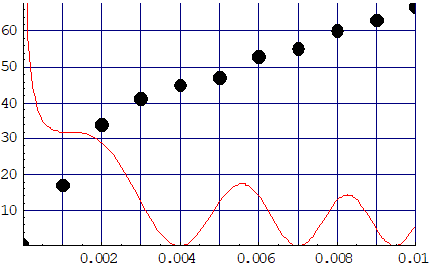
当rot = 81 时,具有反引力场作用量子的波峰过密,使得反引力场作用量子的效果难以显示出来,只有具有普朗克作用量子的波峰能够显示出来.

第6.8节的不确定关系是

Δx Δp ≥ (ħ' / 2) ;

因此有如下关系式:

Δx ≥ h' / [ 4  Δ( m_gfm v ) ] ; ( 4 )

将( 3 )和( 2 )式代入( 4 )式得到

Δx ≥ ( 0.27 G M² v / c² ) / ｛ 4  Δ［ (M v² / c²) v ］｝ ,

Δx ≥ ( 0.27 G M² v / c² ) / ［ 4  (M v² / c²) v ］ ,

Δx ≥ 0.27 G M / ( 4  v² ) ; ( 5 )

Δx是位置的不确定量,也是自旋的时空台阶的直径.时空的自旋台阶对于物体进行惯性系拖曳.

当 h' 变化时,普朗克长度、普朗克时间和普朗克质量都随之变化;"时空点"的概念也随之变化.

7.10.2 天王星和海王星轨道的偏离

天王星和海王星受到太阳的引力小,因此星际的反引力场容易影响天王星和海王星, 导致它们的轨道的不规则性.

7.10.2.1 天王星

天王星的质量是地球质量的14.535倍,即

M = 5.9742 × 10²⁴ ×14.535 kg .

天王星的轨道运动平均速度是

v = 6.81 × 10³ m s^-1 .

将M和v的数值代入( 3 )式得到

h' = 1.03 × 10²⁸ m² kg s^-1 .

将M和v的数值代入( 5 )式得到

Δx ≥ 2.68 × 10⁶ m .

这是天王星轨道偏离的理论值.观测值是

Δx = 2.8 × 10⁶ m .

7.10.2.2 海王星

海王星的质量是地球质量的17.141倍,即

M = 5.9742 × 10²⁴ ×17.141 kg .

海王星的轨道运动平均速度是

v = 5.43 × 10³ m s^-1 .

将M和v的数值代入( 3 )式得到

h' = 1.14 × 10²⁸ m² kg s^-1 .

将M和v的数值代入( 5 )式得到

Δx ≥ 4.98 × 10⁶ m .

这是海王星轨道偏离的理论值.观测值是

Δx = 4.4 × 10⁶ m .

7.10.3 银河系的旋臂之间的距离

银河系的质量主要存在于4个主要的旋臂之中.银河系的质量是2 × 10¹²个太阳质量,因此它的每个旋臂的质量大约是M = ( 1.9891 × 10³⁰ ) × [ 1/4 × ( 2 × 10¹² )] kg.根据奥尔特公式,在太阳处的银河系自转速度是(25 kms^-1 kpc^-1 × 7.1 kpc),即v = 1.775 × 10⁵ ms^-1 .

将M和v的数值代入( 3 )式得到

h' = 3.5 × 10⁶¹ m² kg s^-1 .

将M和v的数值代入( 5 )式得到

Δx ≥ 4.5 × 10¹⁹ m ,

即

Δx ≥ 4.8 × 10³光年 ,

或

Δx ≥ 1.5 千秒差距 .

这是银河系旋臂之间距离的估计值.

在太阳处旋臂之间的距离的观测值与上面的数值接近.

7.10.4 巨洞的直径

时空的自旋台阶对于物体进行惯性系拖曳.

在宇宙的大尺度结构中,巨洞是时空的自旋台阶.

本超星系团的总质量约为10¹⁵倍太阳质量.作为粗糙的近似,取本超星系团引物团粒子相对于巨洞的速度为银晕绕银心运动的速度, 即50 km/s , 于是有

M = 1.9891 × 10³⁰ × 10¹⁵ kg ,

v = 5 × 10⁴ m s^-1 .

将M和v的数值代入( 3 )式得到

h' = 4.0 × 10⁶⁷ m² kg s^-1 .

将M和v的数值代入( 5 )式得到

Δx ≥ 1.1 × 10²⁴ m ,

即

Δx ≥ 1.2 亿光年

或

Δx ≥ 37.0 百万秒差距 .

这是巨洞直径的估计值.观测到的巨洞的直径为20 ~ 100 百万秒差距.

注释与参考文献

[1] 杨布恩指出,在行星系统中, η 常数的作用相当于原子理论的普朗克常数ħ , 扮演基本作用量子的角色,并且有如下方程:

c / v = λ n n = 1, 2, 3 ... ,

η = λ G M / c ,

其中v是行星轨道平均速率. 
 见杨步恩.行星卫星量子理论导引.第1版.大连理工大学出版社.大连.1996年6月.第27页
和第24页.

7.11 反引力场基本电荷方程

惯性系被反引力场拖曳的物质的精细结构常数不变,这意味着这物质除了具有基本电荷之外还具有反引力场基本电荷.因此有下列方程:

(e' / e )² = h' / h ,

式中e'是惯性系被反引力场拖曳的物质的反引力场基本电荷,e是基本电荷, h'是反引力场作用量子, h是普朗克作用量子.

因此有下列方程:

e' = e ( h' / h )^(1/2) . ( 1 )

方程( 1 )可以叫做反引力场基本电荷方程.

7.12 反引力场电磁波传播反引力场作用量子和时空曲率

惯性系被反引力场拖曳的物体发出的电磁波可以叫做反引力场电磁波.

对于光子存在着下列关系式

E = h ν ;

因此对于反引力场电磁波存在着下列关系式

E = h' ν ,   ( 1 )

式中h’ 是反引力场作用量子.

因此反引力场电磁波具有h' .

因为h’ 可以大于h , 所以反引力场电磁波可以具有

1. 较大的反引力场作用量子,

2. 较大的曲率(因为它的时空的自旋台阶可以比较大),

3. 较大的位置和时间的不确定性,

4. 较大的电磁不确定性^{[1], [2]}

5. 较大的能量和动量(根据方程( 1 ) ),

6. 较大的隧道效应,以及

7. 较大的真空遂通效应,即平行宇宙之间较大的隧道效应^[3].

万有引力是通过引力场物质波,即反引力场波来传播的(请参看第2章第2.2节).引力场物质波的h' 可以很大,因此反引力场波的h' 可以很大,由于电磁不确定关系^{[1], [2]} , 反引力场波不能保持电磁中性,因而会变成反引力场电磁波.根据反引力场作用量子方程, h'与万有引力有关.因此反引力场电磁波传播时空曲率(万有引力).

所以反引力场电磁波可以传播

1. 反引力场作用量子,

2. 时空曲率(万有引力),

3. 较大的时空不确定性,

4. 电场和磁场的较大的不确定性,

5. 较大的真空能密度,

6. 较大的时空隧道效应.

反引力场发动机、类雾体、天上的星星和人都可以发出反引力场电磁波.

注解和参考文献

[1] 李·斯莫林.通向量子引力的三条途径.李新洲,翟向华,刘道军译. 
上海科学技术出版社,2003年3月第1版.第57页.
[2] 薛晓舟.量子真空物理导引.科学出版社,2005年8月第一版.第 
 40页.
[3] 同上,第16页.

7.13 反引力场电磁波的速度

反引力场电磁波向真空中的引力场物质,也就是向真空传播反引力场作用量子h' 和时空曲率.所以真空具有h' .由于电磁场中的和量子光学中的不确定关系^{[1], [2], [3]} ,与磁学中温度变化的作用相似, h' 的变化可以使得真空介电常量和真空磁导率变大或者变小,于是真空中反引力场电磁波的速度可以小于c或者大于c ,这意味着时间可以流逝得比较慢或者比较快.

[1] 李·斯莫林.通向量子引力的三条途径.李新洲,翟向华,刘道军译. 
上海科学技术出版社,2003年3月第1版.第57页.
[2] 薛晓舟.量子真空物理导引.科学出版社,2005年8月第一版.第 
 40页.
[3] D. F. Walls, G. J. Milburn, Quantum Optics, Springer-Verlag, 
 Berlin Heidelberg, 1994, pp. 16, 288, 313.

7.14 反引力场电磁学实验

7.14.1 h'与电磁波信号电压的变化频率

反引力场中的电压可以用数字式万用电表(其交流电压的最小分辨力应等于或好于0.1mV)来测量.

将上述数字式万用电表的功能/范围旋钮拨到测量交流电压的最小档,就可以测出空中电磁波信号的电压数值.这个数值在时时变化着.

实验技巧如下.

(1) 如果这个数值的变化太慢,可以先打开窗子,打开电视机,造成一个使得这个数值变化较快的环境,然后再进行实验.可以将两支表笔并排放置.

(2) 为了避免人体的干扰,将万用电表留置在小船上面.

7.14.1.1 小的h'

在第一章记述的实验中,将原自转体换为质量较小的自转体.当"小船"在水面上由于反引力场而运动时,将数字式万用电表的表笔放在自转体的前面,表笔与电机轴垂直.大约两分钟以后可以看到电压数值的变化频率被降低了.这是由于对于该自转体, h' < h (计算方法请见第7.10.1节的方程(3)),这使得局域空间中的电磁不确定度减小了.  

7.14.1.2 较大的h'

如果在上述实验中使用质量较大的自转体,可以发现当h' 较大时,在局域空间中电磁波信号的电压数值的变化频率较高.这是由于当h' 较大时,局域空间中的电磁不确定度增加了.

7.15 反引力场光学实验

7.15.1 h' 的改变导致粒子能级改变

在7.14.1节的实验中,用细棍止住小船的运动以便使得反引力场消失(请参看第二章的方程组(16)),大约两分钟以后可以发现在小船前面电磁波信号的电压数值降低了一点儿.

这是因为在止住小船的运动之前,小船位于反引力场中并且h' < h ;这使得局域空间中粒子的能级升高,造成粒子数反转,于是产生了另一种激光.

在西藏发现的虹化现象可能与此有关.

实验技巧如下.

将一根木尺平放在澡盆的上边缘上,当小船行至木尺时,反引力场消失(请参看第二章的方程组(16)).

7.15.2 h' 的改变导致折射率改变效应

(请点击这里看照片.)

7.15.2.1 在第一章所记述的实验中,在小船的前面放入水中一根细棍,在小船的后面打开台灯.可以观察到当小船由于反引力场而在水面上运动时,大约两分钟以后,细棍在澡盆侧壁上的影子的水下部分向窗户的方向略微移动了一点儿.(实验时应将实验室的门和实验室内的计算机关闭.)

这是由于在小船前面的局域空间中, h' < h .在窗户附近电磁波信号的电压数值较小,使得h' 容易在局域空间中占主导地位.因此在水面上方窗户方向的局域空间中媒质的折射率最小,水面下方与窗户相反方向的局域空间中媒质的折射率最大.光线向光密媒质的方向折射,也就是向背离窗户的方向移动了,因此影子向着窗户的方向移动了.

7.15.2.2 但是有时在窗户附近电磁波信号的电压数值大于房间较里面的部分的电磁波信号的电压数值,这时在上述实验中就会观察到影子向背离窗户的方向移动了.

7.15.2.3 实验技巧如下.

(1) 为了便于比较,可以采取如下办法.

(1.1) 使用数码相机拍摄实验照片.

(1.2) 使用Photoshop软件中的选择和移动工具,将每张实验照片中的阴影区移动并且并排放置到一个新建的空白图像文件(这里叫做照片C)中.新建图像文件的方法是选择"文件"菜单中的" 新建".

(1.3) 使用Photoshop中的缩放工具将照片C放大.

(2) 为了使阴影的边缘清晰,可以采取如下办法^[1].

(2.1) 将两张不透光的纸放在光源的前面,使光源形成狭缝光源.

(2.2) 阴影与细棍的距离最好是阴影与光源的距离的一半.

参考文献

[1] 李桂春.气动光学.国防工业出版社,2006年1月第1版.第356—358页.

7.16 反引力场电磁学方程和反引力场光学方程

根据电磁场的量子化理论、电磁波速度公式、斯涅耳定律，以及第7.14节和第7.15节所叙述的实验的结果,可以建立起下列方程:

h_a / h = F’_cv / F_cv ; ( 1 )

h_a / h = ( n’ / n )² ; ( 2 )

式中h_a是局域反引力场中作用量子的平均值, h是普朗克常量, F’_cv 是局域反引力场中电磁波信号的电压数值的变化频率, F_cv是没有反引力场时电磁波信号的电压数值的变化频率,n是折射率,n’是局域反引力场中的折射率.

7.17 反引力场德布罗意波

根据第7.10.1节,实验显示出在反引力场中一个粒子具有平行的作用量子h和h' .因此在反引力场中一个粒子具有并且联系着平行的德布罗意波.根据波粒二象性,这些波对应着平行的引物团粒子(请参看第4章).这些平行的引物团粒子具有不同的作用量子并因而具有不同的时间流逝速度(请参看第7.13节).

因此当h’<h时存在着”预言”这种现象.(请参看第6.13节)

7.18 反引力场热学实验

在第一章所记述的实验中,使用分辨率等于或好于0.1°C的数字温度计.使用质量小的自转体使得对于该自转体, h' < h (计算方法请见第7.10.1节的方程(3)).

将”小船”因反引力场而运动时小船表面的温度和用细棍将小船止住从而使反引力场消失时(请参看第二章的方程组(16))小船表面的温度相比较.在扣除热流起伏(即温度噪声)的因素后,可以观察到前者在多数情况下高于后者约0.1°C或更多.

这是由于存在着下列关系式

E’ = h’ ν , ( 1 )

式中E’是引物团粒子的反引力场能量, h’ 是反引力场作用量子, ν 是引物团粒子的频率.

由上式可以看出h’标示着反引力场能级.当粒子由反引力场作用量子为h’₁ 的时空跃迁到反引力场作用量子为h’₂ 的时空的时候,如果h’₁ > h’₂ ,则粒子释放反引力场能量(包括非现在时反引力场能量),粒子的温度升高;如果h’₁ < h’₂ ,则粒子吸收反引力场能量(包括非现在时反引力场能量),粒子的温度降低.

一个天体的引物团粒子极其巨大,它具有量子化的分层结构,其中心的h’大于其外层的h’ (计算方法请见第7.10.1节的方程(3)).

《量子天文学》认为天体象一个重原子,粒子从天体的内部跃迁到表面时放出能量,温度升高,从天体的表面跃迁到内部时吸收能量,温度降低^[1].

实验技巧如下.

(1) 为了避免读数起伏,使用热电偶温度计,不使用电阻温度计.

(2) 为了避免人体的干扰,将温度计留置在小船上面.

参考文献

[1] 肖钦羡,窦剑文.量子天文学.兰州大学出版社,2005年1月第一版,第8页,第31页.

7.19 引物旋涡能放大磁场

粒子跃迁时,它放出或吸收能量为h’ν的引物旋涡.

引物旋涡本身没有磁场,但是因为它具有惯性系拖曳效应,所以在有初始磁场的情况下,它能分离正、负离子(根据左手定则),并且由于漩涡中心的运动速度大于其边缘的运动速度,引物旋涡能放大初始磁场(根据右手螺旋定则),例如因电磁测不准原理而产生的初始磁场.

UFO和百慕大三角的秘密可能与此有关.请参看第六章的第6.22和6.21节.

注释和参考文献:

《量子天文学》认为,太阳黑子本身没有磁场,但是因为它能拖曳离子,所以在有初始磁场的情况下,黑子旋涡能分离正、负离子(根据左手定则),并且因为黑子漩涡中心的运动速度大于其边缘的运动速度,所以黑子能放大初始磁场(根据右手螺旋定则). ^[1]

[1] 肖钦羡,窦剑文.量子天文学.兰州大学出版社,2005年1月第一版,第33,34页.

7.20 反引力场磁学实验

在第三章记述的实验中,在自转体的前面(小船的船头)放置一个罗盘.小船处于水平.电池应是新充过电的.

第一步. 使自转体沿顺时针方向转动.船头指向东南.当小船因反引力场而运动时,大约2分钟以后可以观察到罗盘指针的南极向西偏转了约2°.

第二步. 使自转体沿逆时针方向转动.船头再次指向东南. 当小船因反引力场而运动时,大约2分钟以后可以观察到罗盘指针的南极向西偏转了约2°.

第三步. 使自转体沿逆时针方向转动.船头指向西南. 当小船因反引力场而运动时,大约2分钟以后可以观察到罗盘指针的南极向东偏转了约2°.

第四步. 使自转体沿顺时针方向转动.船头再次指向西南.当小船因反引力场而运动时,大约2分钟以后可以观察到罗盘指针的南极向东偏转了约2°.

　　上述实验显示出自转体的引物旋涡放大了来自地磁场的初始磁场(在地球的北极附近是地磁场的南极,在地球的南极附近是地磁场的北极).

7.21 阴阳、特异功能与h'

中医中的阴意味着具有或导致较小的h' ,而阳则意味着具有或导致较大的h' .

特异功能者具有较强的改变h' 的能力.

7.22 每个量子态具有它不同的反引力场作用量子

引力场物质决定量子的时空几何结构(参看第6.5节),并且当外力足够小时(参看第一章方程(1))使得量子处于反引力场中.每个量子态具有它不同的反引力场作用量子(参看第7.10.1节的方程(3)).因此不同的量子态处于不同的反引力场和不同的时空之中(参看第7.12节).在测量中,由于第一章中的方程(2),反引力场消失,从而导致反引力场作用量子的消失和时空的塌缩.

每个反引力场作用量子对应着一个不同的时间维.(参看第7.9节的(3)).因此每个量子态对应着一个不同的时间维.当量子从一个量子态跃迁到另一个量子态时,它会吸收或放出一定量的能量(参看第7.18节).

7.23 从中得出第一章方程(2)的实验

用玩具电动机带动一个大圆纸板以适当的速度水平地自转,纸板的重量并不减小,从这个实验可以得出第一章的方程(2).

7.24 在反引力场实验中秒表的时间有时短暂停止

7.24.1 实验步骤

(1) 准备三块完全一样的电子秒表(性能:潜水表,精确度1/100秒,最长可测24小时).把它们分别叫做秒表A,秒表B和秒表C. (请点击这里看照片.)

(2) 同时起动A、B两块秒表.将秒表B平放在反引力场发动机的自转体的前面(在没有脸盆的小船的船头).没有脸盆的小船水平地放在澡盆里的水面上.

为了使得小船的速度不等于零,澡盆里的水应新鲜洁净,电池应是新充过电的,天气应晴朗.

开动电机.将秒表A放在另一间屋子里面的桌子上.

16个小时以后将秒表A和秒表B并排放置.对秒表A和秒表B的读数拍摄录像和至少10张照片,拍摄照片时快门使用1/1000 s.

(3) 同时起动A、C两块秒表.在第一章第1.2节所述的实验中,将秒表C平放在反引力场发动机自转体的前面(即放在小船的船头).将"小船"放在凳子上.开动电机.由于凳子面的摩擦阻力大,根据第一章的方程(2),这时反引力场为零.将秒表A放在另一间屋子里面的桌子上.

16个小时以后将秒表A和秒表C并排放置.对秒表A和秒表C的读数拍摄录像和至少10张照片,拍摄照片时快门使用1/1000 s.

7.24.2 实验结果

(1) 慢速播放和步进式播放的录像显示出,与秒表A和秒表C显示的时间相比,秒表B显示的时间有时短暂停止.(请点击这里看录像.)左边是表A.右边粘有一块橡皮膏的是表B.为了节省时间,请点击"保存"而不是"打开".)录像文件是100_4960.MOV.

(2) 当秒表A接近秒表B时,秒表A会受到秒表B的影响,秒表A所显示的时间不确定程度会因而略有些增加.

7.24.3 理论

(1) 在反引力场中,不同的反引力场作用量子对应着不同的时空不确定度并因而对应着不同的时空.在反引力场中,当粒子的质量和速度由于量子力学中的不确定关系以及由于量子态的改变而变化的时候,粒子具有不同的反引力场作用量子并因而处于不同的时空之中.

因此在反引力场里,在一些瞬间秒表B处于其他时空中的一个量子态,因此秒表B显示的时间就暂停了.

在秒表B离开反引力场以后,秒表B的上述走时特性会持续一段短时间.

(2) 根据力学,

ΔE = (1/2) m v² . ( 1 )

根据第7.10.1节的方程( 2 ),

m = M v² / c² , ( 2 )

式中m是反引力场发动机的自转体的引物团粒子的质量.

根据第7.10.1节的方程( 3 ),

h' = 0.27 G M² v / c² , ( 3 )

式中h'是反引力场作用量子.

根据第6.8节的方程( 2 ),

Δt ΔE ≥ ħ' / 2 . ( 4 )

由方程( 1 ), ( 2 ),( 3 )和( 4 )得到

Δt ≥ 0.135 G M / ( v³) ,

（v 不等于0） , ( 5 )

式中Δt是时间的不确定量, G是牛顿引力常数,M是反引力场发动机自转体的质量, v是因反引力场而运动的小船的速率.

在上述实验中, M = 0.00315 kg, v 约等于0.00004 m/s , Δt 约等于0.14 s .

7.25 水是时空变换的催化剂

在反引力场实验中,如果小船的载重量不大,承载装置就最好不包括脸盆,而是将泡沫塑料板直接放在水面上.这样反引力场效应比较容易发生.

这是因为在第四章所记述的反引力场实验中,水分子的时间不确定性可以达到

Δt = 239 天 .

请参看第六章第6.21节.

7.26 反引力场非定域时空实验

7.26.1 理论

7.26.1.1 由第7.10.1节和第7.24.3节可以知道存在着下列三个关系式:

h' = 0.27 G M² v / (c²) ,   (1)

(a ≠ 0) , (1)

Δt ≥ 0.135 G M / ( v³) ,

(a ≠ 0) , (2)

和

Δx ≥ 0.27 G M / ( 4  v² )

(a ≠ 0) , (3)

式中a是反引力场加速度(请参看第2.3节), h' 是反引力场作用量子,M是物体的质量,v是物体的速度.

由此可以知道,在反引力场中物体的时空定域在变化着.

例如在下列实验中,近似地有如下数值:

M = 0.00315 kg ,

v = 0.00004 m/s ,

h' = 7.96×10^-38,

Δt≥1.4×10^-1秒,

Δx≥2.8×10^-6 米.

7.26.1.2 宇宙在加速地反引力膨胀.地球及地球上的物体处于宇宙的反引力场中.宇宙的质量M极大.根据哈勃定律,在地球上某物体处宇宙空间膨胀的速度v极小,而在观测者处v和(dv/dt)都是零.

因此根据本节开始处的三个关系式可以知道,在使得宇宙空间膨胀的反引力场中,观测者以外的物体的时空定域具有极大的不确定性,观测者以外的物体具有现在时空和非现在时空.

7.26.1.3 但是如果一个观测者位于因反引力场发动机的工作而运动的小船上,那么这个观测者的情况就会有所不同.这个观测者的反引力场加速度不等于零.于是根据本节开始处的三个关系式可以知道,这位观测者的时空定域具有较大的不确定性, 这位观测者具有现在时空和非现在时空,并且能在现在时空中和非现在时空中与物体相互作用.

因此反引力场小船是连接现在时空与非现在时空的时空隧道.

在7.26.2节描述的实验中,纸片起到了观测者的作用.

因此,

当 h' = 0时,

观测者观测到物体在时空方面是定域的;

当 h' ≠ 0时,

观测者观测到物体在时空方面是非定域的;

式中h' 是观测者的反引力场作用量子.

7.26.1.4 观测者的Δt有些类似于摄影中的曝光时间和光圈.如果观测者A的Δt比观测者B的Δt大,则与观测者B的情况相比,

(1) 观测者A与非现在时空中的物体的相互作用较强,较明显,

(2) 观测者A观测到物体的Δt和Δx较大,因此观测者观测到的物体较虚.

7.26.1.5 命反引力场发动机的工作导致的时间不确定性是Δt ,则反引力场发动机周围的众时空区域的时间不确定性会变得接近于Δt ;这会使得这些时空区域中的物体的时间不确定性变小或变大以便接近于Δt ;也就是说,反引力场发动机的工作具有双向效应.

7.26.2 实验

7.26.2.1 实验1

请点击这里看照片.

7.26.2.1.1 实验步骤

(1) 准备一张要放在较高位置的空白稿纸的纸片(以下称作上纸片).

(2) 在纸片的正面用黑色签字笔画上阿拉伯数字2的图形.(请点击这里看照片.)

(3) 将纸片正面向上地放在玻璃瓶罐(请参看第1.2节)里面的底部,在电动机底座的下面.

(4) 准备一个能容纳一张3.5"软盘的塑料盘盒(以下称作盘盒).

(5) 准备一张要放在较低位置的空白稿纸的纸片(以下称作下纸片).将它正面向上地放在盘盒里.关闭盘盒.

(6) 将盘盒和电池放在泡沫塑料板的上面.将瓶罐放在盘盒的上面.

(7) 将泡沫塑料板放在澡盆里的水面上.借助于水平仪,调整盘盒和电池的位置使得泡沫塑料板水平.

(8) 启动电动机,实验就开始了.(请点击这里看录像.)录像文件是100_6587.MOV.

为了减小|Σa' |(请参看第2章第2.3节),或者说,为了避免使反引力场加速度过于频繁地变为零,实验不应长时间暴露在强光下.

(9) 在实验的过程中可以将实验暂时停下来以便观察纸片和换用新充好电的电池.暂停的时间不算在实验的持续时间之内.

(10) 象观察纸币上的水印那样迎光观察纸片.

将纸片顺时针或逆时针旋转90°、180°或270°,然后对纸片进行观察.

7.26.2.1.2 实验结果

(1) 当试验延续了28小时的时候,可以看到在下纸片的正面在中部有一个看着象水印般的数字2的图形.随着实验时间的延长,这个水印般的数字2的图形变得越来越清楚.

(2) 当实验延续了48小时的时候,可以看到在上述的水印般的数字2的图形的左边出现了一个较小的水印般的数字2的图形.

(3) 在较大的水印般的数字2的图形的右上方出现了一个小的水印般的数字3的图形(请点击这里看照片6571). (纸片后面的背景光是白炽光,白炽光偏于红色.) (请点击这里看一张对照样本的照片.)

(4) 在实验过程中,当一张纸片相对于另一张纸片的位置略微变动了以后,上纸片上面的图形仍能找到下纸片上面的水印的般图形的位置(即自动跟踪),这使得水印般的图形变得越来越清晰,

这显示出水印般的图形有它自己的时空曲率,并因此有它自己的质量.这说明水印般的图形不仅是信息,而且是物质.

(5) 当"小船"由于反引力场发动机的工作而开始运动以后,它可能会在离澡盆盆边不远的地方长时间地滞留.实际上这时小船是在势垒区域中运动(请参看第7.3.1节),它的反引力场加速度虽然很小,但并不是零.在这种情况下,上述实验结果仍然会出现.

7.26.2.1.3 实验分析

上纸片和下纸片的时间定域和空间定域在"小船"的反引力场中都变化了,因此在非现在时空里两张纸片发生了相互作用(请参看第6.13节),看起来好象是上纸片上的数字2的图形穿透了玻璃瓶罐、粘在瓶底外部的一层门窗密封条(请点击这里看照片)和塑料盘盒并到达了下纸片.

7.26.2.2 实验1的一些变例

7.26.2.2.1 实验2

(1) 在一张下纸片上用黑色签字笔画上数字3的图形(请点击这里看照片.)上纸片是一张空白稿纸的纸片.

上纸片的照片上显示了实验结果的这次实验持续了163小时.请点击这里看录像).录像文件是100_6689.MOV.

(2) 实验结果(请点击这里看照片.)

在上纸片的左下部出现了一个比较大的暗色的水印般的数字3的图形.

在镊子的左上方有一个暗色的水印般的单词"age"(antigravitation engine)的图形.单词age的图形是在上述实验1以前的一次实验中写在一张纸片上的(请点击这里看补拍的照片),这张纸片在那次实验中放在了玻璃瓶罐外侧底面的下面,在两张空白纸片之间;在实验2开始的28天4小时以前,也就是实验1开始的8天17小时以前,这三张纸片就已经被拿走了.实验2中使用的上、下纸片都是另外的纸片.

在上纸片的右上边缘处有一个明亮的水印般的图形" ⓢ ".图形" ⓢ "原是在实验2结束了118小时45分以后开始的一个实验中画在下纸片上的图形(请点击这里看照片).使用这个图形是因为它看起来有点像太极图.

(3) 事件本身的时间顺序如下.

(3.1)

2007-2-26 在一张纸片上写单词”age”的图形

2007-2-26—2007-2-28 一个实验,其中使用了写有图形”age”的纸片

2007-2-28 写有图形”age”的纸片被拿走

(3.2)

2007-3-8—2007-3-15 实验1

(3.3)

2007-3-28—2007-4-5 实验2

2007-4-5 实验2中使用的纸片被拿走

(3.4)

2007-4-10 在一张纸片上画图形”ⓢ”

2007-4-10—2007-4-15 一个实验,其中使用了画有图形”ⓢ”的纸片

(3.5)

2007-5-18 在实验2的上纸片上暗色的水印般的图形”age”被发现

2007-5-27 在实验2的上纸片上明亮的水印般的图形”ⓢ”被发现

(4)  反引力场发动机把"age"和"ⓢ"这两个非现在时空的图形变成了现在时空的图形(参看第7.26.1.5节).

7.26.2.2.2 实验3

使用密封饭盒代替玻璃瓶罐;将电池也放入这个饭盒中.

可以得到相似的实验结果.

7.26.2.2.3 实验4

在软盘盒上面放置一个双面镜,或者一个轻的铝盆(请点击这里看照片).

可以得到相似的实验结果.

7.26.2.3 对照实验

不是将泡沫塑料板放在澡盆里的水面上,而是将它搭放在一个充满水的小盆的上边缘上,或者将泡沫塑料板放在桌子上的一个垫子上面.

其它步骤与实验1相同.

在对照实验中得不到上述实验结果.

7.26.3 分析

上述实验现象可以分解成以特异方式出现的下列现象:

透壁、移物、取物、变形、透视、遥感、分身、自动跟踪、重现、预现、改变物质(纸纤维)的密度.

7.27 反引力场非定域数学实验

7.27.1 实验步骤

请点击这里看照片.

(1) 准备一张要放在较高位置的空白稿纸的纸片(以下称作上纸片).

(2) 将上纸片正面向上地放在玻璃瓶罐(请参看第1.2节)里面的底部,在电动机底座的下面.

(3) 准备一个能容纳一张3.5"软盘的塑料盘盒(以下称作盘盒).

(4) 准备一张要放在较低位置的空白稿纸的纸片(以下称作下纸片).用签字笔将”3+2=?”写在下纸片上.请点击这里看照片.

将下纸片正面向上地放在盘盒里.关闭盘盒.

(5) 将盘盒和电池放在泡沫塑料板的上面,将瓶罐放在盘盒的上面,在电池的前面.

(6) 将泡沫塑料板放在澡盆里的水面上.借助于水平仪,调整泡沫塑料板上面的物体的位置使得泡沫塑料板水平.

(7) 启动电动机,实验就开始了.

为了减小|Σa'|(请参看第2章第2.3节),或者说,为了避免使反引力场加速度过于频繁地变为零,实验不应长时间暴露在强光下.

(8) 在实验的过程中可以将实验暂时停下来以便观察纸片和换用新充好电的电池.暂停的时间不算在实验的持续时间之内.

(9) 实验结束后,象观察纸币上的水印那样迎光观察上纸片并对纸片照相.

(10) 如果照片中的信息不够清晰,可以使用Photoshop的"图像->调整->亮度/对比度"命令、"图像->调整->色调分离"命令和"窗口->通道"->"绿"或"蓝"或"红"命令来处理照片中的图像.

(11) 使用Photoshop的命令"图像->旋转画布"将纸片的图像逆时针或顺时针旋转90°、180°或270°,然后观察图像.

7.27.2 实验结果

在上纸片的照片上显示了实验结果的这次实验持续了135小时31分.

请点击这里看上纸片的照片,图像未经处理. (上纸片后面的背景光是白炽光,白炽光偏于红色.)

可以看到在上纸片的正面在中部有一个看着象水印般的数字5的图形.

第一章 介绍一个人人能做的反引力场发动机实验　

第二章 反引力场发动机方程组的建立

第三章 反引力场力学实验技巧和应用范围

第四章 实验数据分析(宏观量子现象的检验)

第五章 实验数据分析(主要是为了检验第一章的方程（１) ）

第六章 一种新的物态—类雾态

第七章 反引力场实验(续)

第七章的实验照片